**This is an old revision of the document!**
ASCII_Analysis.ipynb
This Jupyter notebook, titled 'ASCIIAnalysis.ipynb', is a comprehensive analysis tool designed for the exploration and statistical study of ASCII data related to dance movements and the associated emotional states. The script includes functionalities for data preprocessing, visualization, and the extraction of meaningful statistics from time-series data. Through various statistical and signal processing techniques such as Lomb-Scargle periodograms and Gaussian fitting, it investigates properties like the center of position evolution, average distance from center, velocity analysis, and frequency domain analysis to discern patterns correlated with different emotions in dance movements. The notebook utilizes libraries such as pandas, matplotlib, numpy, scipy, seaborn, and mplEasyAnimate for its analysis.
python
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from tqdm import tqdm
import numpy as np
from mplEasyAnimate import animation
from scipy.signal import lombscargle
import os
from scipy.optimize import curve_fit
import seaborn as sns
python
def frameToArray(frame):
start = 1
vecs = np.zeros(shape=(int((frame.shape[0]-1)/3), 3))
for itr, end in enumerate(range(4, frame.shape[0]+3, 3)):
vecs[itr] = np.array(frame[start:end])
start = end
return vecs
python
def CalcCenterOfPos(frame):
vecs = frameToArray(frame)
return vecs.mean(axis=0)
python
def CenterOfPosEvolution(df):
COPs = np.zeros(shape=(df.shape[0], 3))
times = df['Time'].values
for itr, frame in tqdm(df.iterrows(), total=df.shape[0]):
COPs[itr] = CalcCenterOfPos(frame)
return COPs, times
python
def getAvgPosFromCenter(frame):
COP = CalcCenterOfPos(frame)
vecs = frameToArray(frame)
return np.abs(vecs-COP).mean(axis=0)
python
def getAvgDistFromCenter(frame):
COP = CalcCenterOfPos(frame)
vecs = frameToArray(frame)
return np.mean(np.sqrt(np.sum(np.power(np.subtract(COP, vecs), 2), axis=1)))
python
def evolveAvgPosFromCenter(df):
SEPs = np.zeros(shape=(df.shape[0], 3))
times = df['Time'].values
for itr, frame in tqdm(df.iterrows(), total=df.shape[0]):
SEPs[itr] = getAvgPosFromCenter(frame)
return SEPs, times
python
def evolveAvgDistFromCenter(df):
SEPs = np.zeros(shape=(df.shape[0],))
times = df['Time'].values
for itr, frame in tqdm(df.iterrows(), total=df.shape[0]):
SEPs[itr] = getAvgDistFromCenter(frame)
return SEPs, times
python
def genLSP(t, y, s=None):
nyquist = 1/(2*(t[1]-t[0]))
res = (t[1]-t[0])/t.shape[0]
if not s:
s = int(1/res)
f = 2*np.pi*np.linspace(res/10, 0.5, s)
pgram = lombscargle(t, y, f, normalize=True)
return f, pgram
python
analyzedFiles = os.listdir('AnalyzedData/')
analyzedFiles = ["AnalyzedData/{}".format(x) for x in analyzedFiles if x[0] != '.']
python
emotions = [(x.split('.')[0]).split('_')[-1] for x in analyzedFiles]
python
data = list()
for file in analyzedFiles:
analysis = np.load(file)
data.append(analysis)
python
for i, element in enumerate(data):
data[i][1] = (data[i][1]-np.mean(data[i][1]))/np.mean(data[i][1])
python
velocities = list()
for dance in data:
vel = (np.roll(dance[1], -1) - np.roll(dance[1], 1)) / (np.roll(dance[0], -1) - np.roll(dance[0], 1))
velocities.append(np.vstack([dance[0], vel]))
python
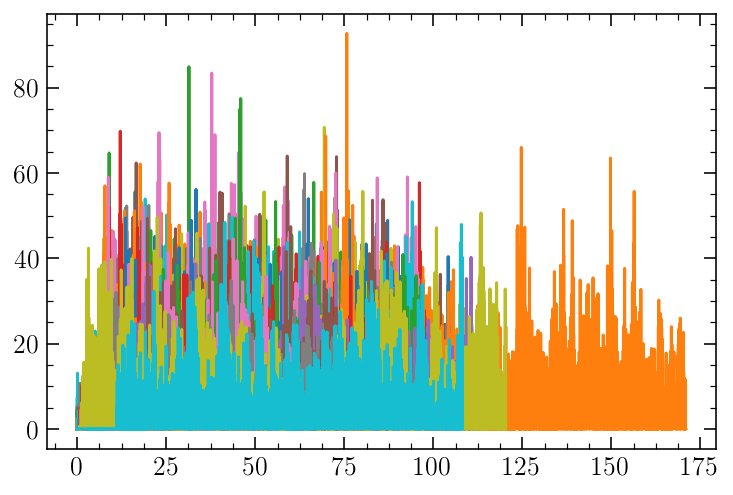
for dance in velocities:
plt.plot(dance[0], abs(dance[1]))
python
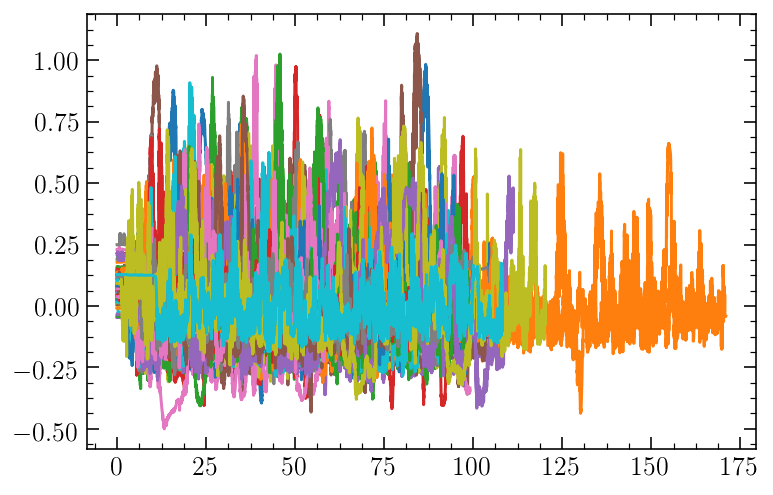
for dance in data:
plt.plot(dance[0], dance[1])
python
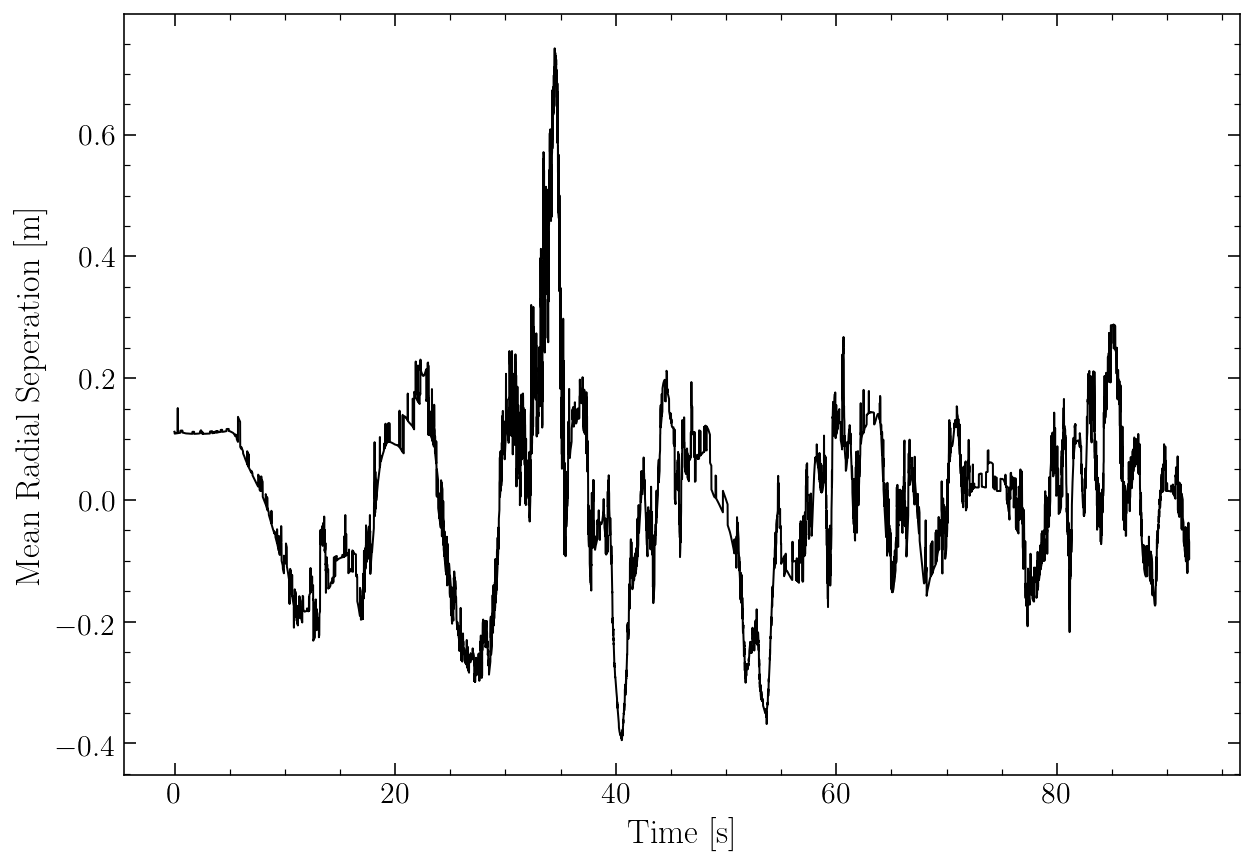
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
ax.plot(data[0][0], data[0][1], 'k', linewidth=1)
ax.set_xlabel('Time [s]', fontsize=17)
ax.set_ylabel('Mean Radial Seperation [m]', fontsize=17)
ax.tick_params(axis='both', which='major', labelsize=15)
plt.savefig("Figures/MeanRadialSeperation.pdf", bbox_inches='tight')
# Frequency Position Analysis
python
FTs = np.zeros(shape=(49, 2, 2000))
python
count = 0
for did, dance in tqdm(enumerate(data), total=len(data)):
if did != 9:
f, pgram = genLSP(dance[0], dance[1], s=2000)
FTs[count, 0] = f
FTs[count, 1] = pgram
count += 1
python
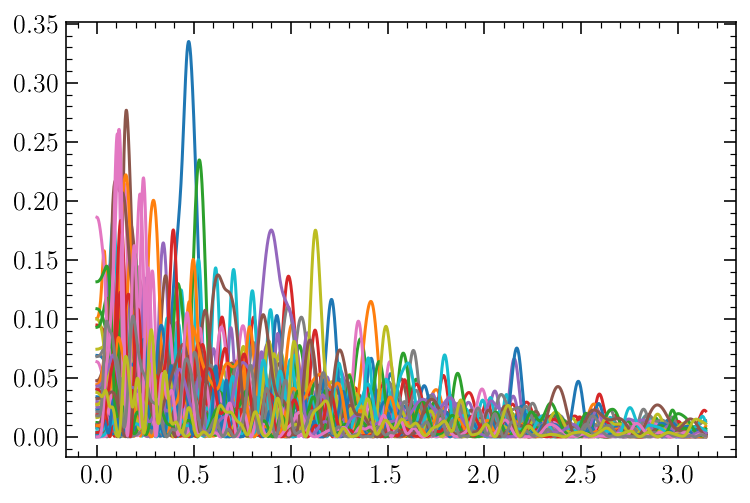
for fid, FT in enumerate(FTs):
if np.mean(FT[1]) > 0.4:
print(fid)
plt.plot(FT[0], FT[1])
python
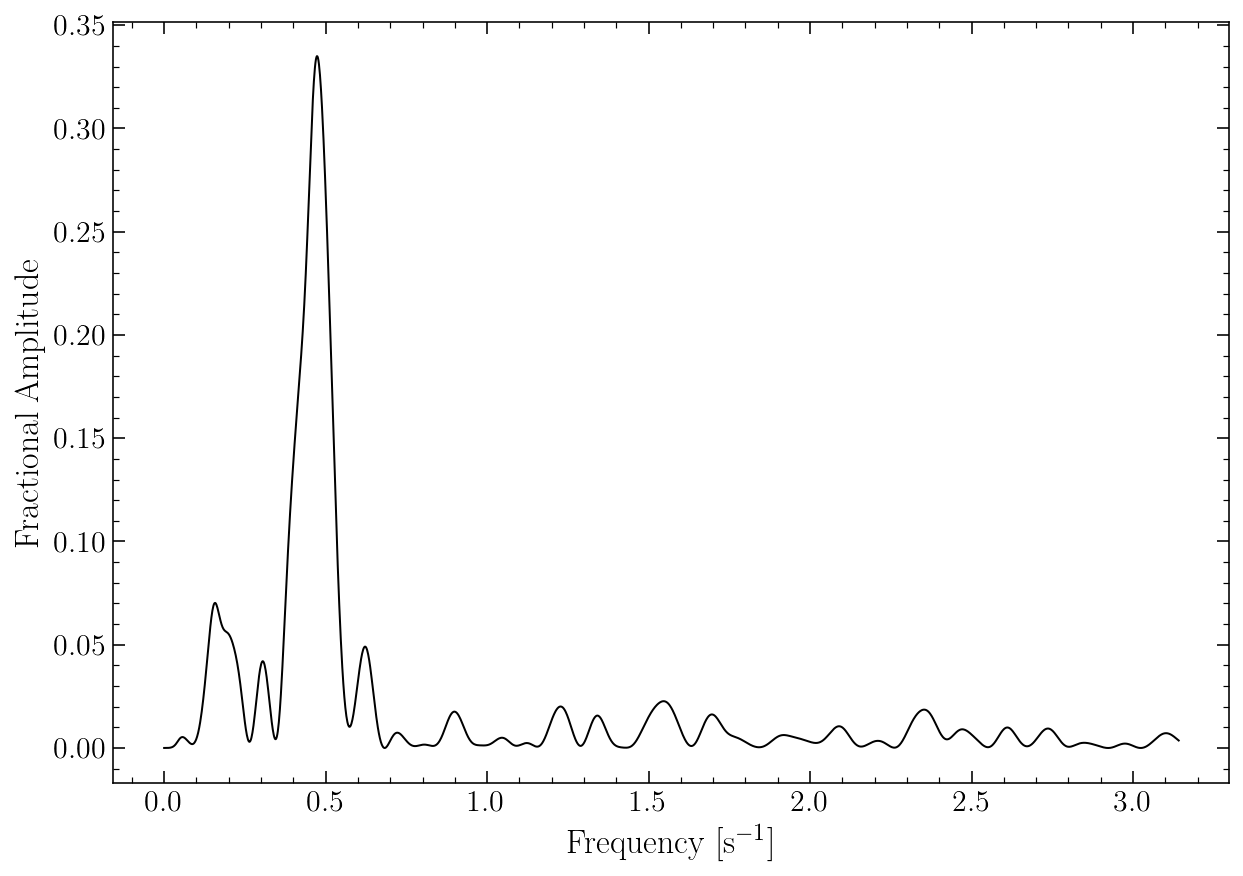
fig, ax = plt.subplots(1, 1, figsize=(10, 7))
ax.plot(FTs[0][0], FTs[0][1], 'k', linewidth=1)
ax.set_xlabel(r'Frequency [s$^{-1}$]', fontsize=17)
ax.set_ylabel('Fractional Amplitude', fontsize=17)
ax.tick_params(axis='both', which='major', labelsize=15)
plt.savefig("Figures/FTExample.pdf", bbox_inches='tight')
python
len(evalEmotions)
49
python
stats = np.zeros(shape=(49, 3))
evalEmotions = list()
count = 0
for fid, FT in enumerate(FTs):
stats[count] = np.array([FT[0][FT[1].argmax()], FT[1][FT[1].argmax()], np.mean(FT[1])])
evalEmotions.append(emotions[count])
count += 1
python
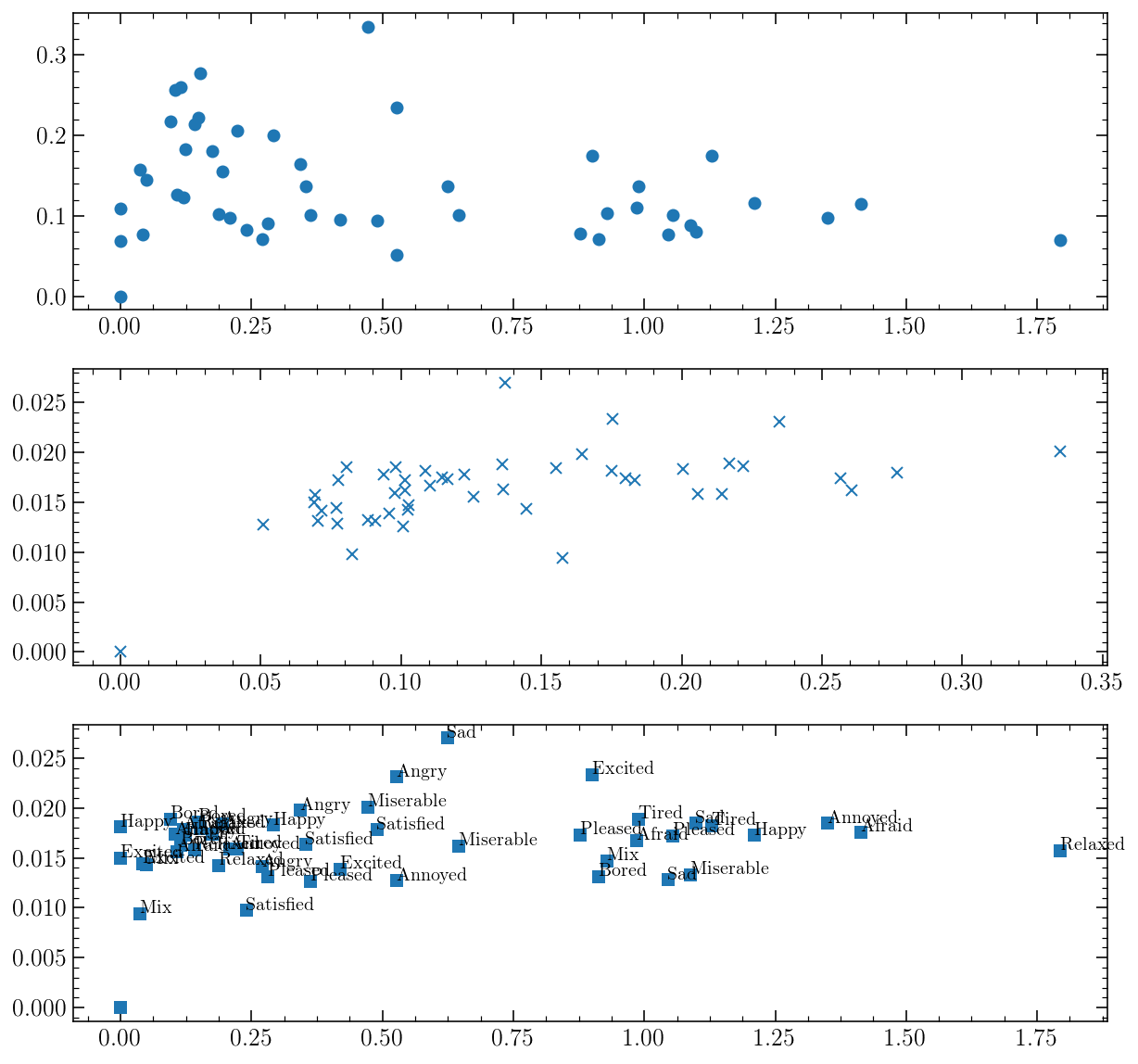
fig, axs = plt.subplots(3, 1, figsize=(10, 10))
axs[0].plot(stats[:, 0], stats[:, 1], 'o')
axs[1].plot(stats[:, 1], stats[:, 2], 'x')
axs[2].plot(stats[:, 0], stats[:, 2], 's')
for stat, emotion in zip(stats, evalEmotions):
axs[2].annotate(emotion, xy=(stat[0], stat[2]))
python
gaus = lambda x, mu, sigma: 1/np.sqrt(2*np.pi*(sigma**2))*np.exp(-((x-mu)**2)/(2*(sigma**2)))
bimodal = lambda x, mu1, sigma1, mu2, sigma2: gaus(x, mu1, sigma1)+gaus(x, mu2, sigma2)
python
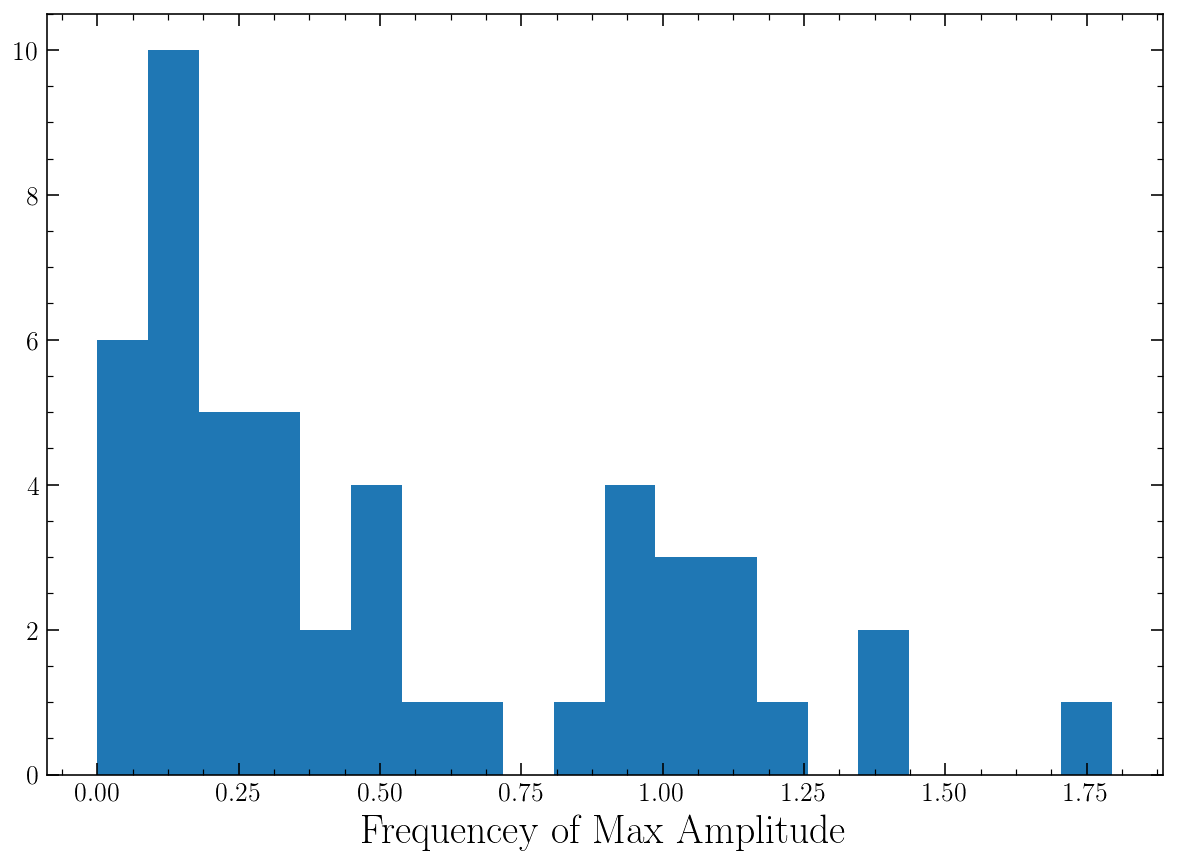
fig = plt.figure(figsize=(10, 7))
bins = plt.hist(stats[:, 0], bins=20)
centers = (bins[1][1:]+bins[1][:-1])/2
plt.xlabel('Frequencey of Max Amplitude', fontsize=20)
Text(0.5, 0, 'Frequencey of Max Amplitude')
python
fit1, covar1 = curve_fit(gaus, centers, bins[0], p0=[0.1, 0.2])
err1 = np.sqrt(np.diag(covar1))
fit2, covar2 = curve_fit(gaus, centers, bins[0], p0=[1, 0.1])
err2 = np.sqrt(np.diag(covar2))
python
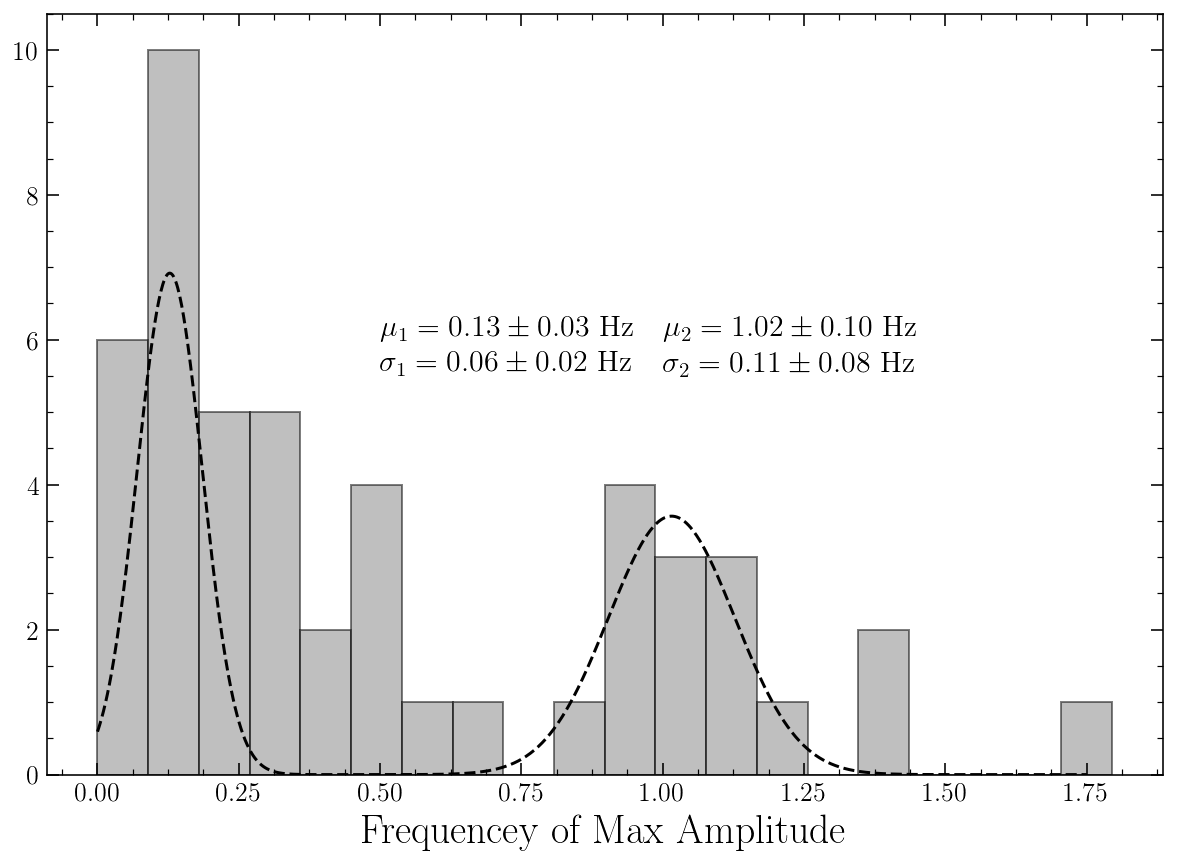
fig = plt.figure(figsize=(10, 7))
x = np.linspace(0, 1.75, 1000)
bins = plt.hist(stats[:, 0], bins=20, color='grey', alpha=0.5, ec='black')
plt.plot(x, gaus(x, *fit1)+gaus(x, *fit2), color='black', linestyle='dashed')
plt.xlabel('Frequencey of Max Amplitude', fontsize=20)
plt.annotate(r'$\mu_{{1}}={:0.2f}\pm{:0.2f}$ Hz'.format(fit1[0], err1[0]), xy=(0.5, 6), fontsize=15)
plt.annotate(r'$\sigma_{{1}}={:0.2f}\pm{:0.2f}$ Hz'.format(fit1[1], err1[1]), xy=(0.5, 5.5), fontsize=15)
plt.annotate(r'$\mu_{{2}}={:0.2f}\pm{:0.2f}$ Hz'.format(fit2[0], err2[0]), xy=(1, 6), fontsize=15)
plt.annotate(r'$\sigma_{{2}}={:0.2f}\pm{:0.2f}$ Hz'.format(fit2[1], err2[1]), xy=(1, 5.5), fontsize=15)
plt.savefig('Figures/FrequencyDist.pdf', bbox_inches='tight')
# Velocity Analysis
python
nonStatGaus = lambda x, mu, sigma, A: A*np.exp(-((x-mu)**2)/(2*(sigma**2)))
python
meanVels = [np.std(x[1]) for x in velocities]
python
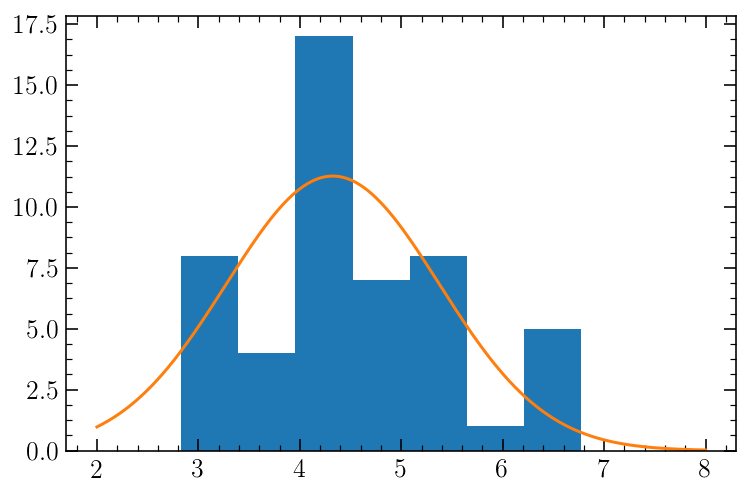
x = np.linspace(2, 8, 1000)
bins = plt.hist(meanVels, bins=7)
centers = (bins[1][1:]+bins[1][:-1])/2
fit, covar = curve_fit(nonStatGaus, centers, bins[0], p0=[4.5, 6, 7])
plt.plot(x, nonStatGaus(x, *fit))
plt.show()
python
timeSeriseStats = np.zeros(shape=(49, 4))
count = 0
for did, dance in enumerate(velocities):
if did != 9:
timeSeriseStats[count, 0] = np.mean(dance[1])
timeSeriseStats[count, 1] = np.median(dance[1])
timeSeriseStats[count, 2] = np.max(dance[1])
timeSeriseStats[count, 3] = np.std(dance[1])
count += 1
python
df = pd.DataFrame(data=timeSeriseStats, columns=['Mean', 'Median', 'Max', 'Sigma'])
df['Emotion'] = pd.Series(evalEmotions, index=df.index)
python
df
<div>
<style scoped>
.dataframe tbody tr th:only-of-type {
vertical-align: middle;
}
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}
</style>
<table border=“1” class=“dataframe”>
<thead>
<tr style=“text-align: right;”>
<th></th>
<th>Mean</th>
<th>Median</th>
<th>Max</th>
<th>Sigma</th>
<th>Emotion</th>
</tr>
</thead>
<tbody>
<tr>
<th>0</th>
<td>-0.001798</td>
<td>-0.004902</td>
<td>56.168820</td>
<td>2.978317</td>
<td>Miserable</td>
</tr>
<tr>
<th>1</th>
<td>-0.001649</td>
<td>0.002063</td>
<td>62.108348</td>
<td>5.054398</td>
<td>Mix</td>
</tr>
<tr>
<th>2</th>
<td>-0.004032</td>
<td>0.006175</td>
<td>44.446849</td>
<td>5.329097</td>
<td>Angry</td>
</tr>
<tr>
<th>3</th>
<td>-0.002111</td>
<td>0.007060</td>
<td>42.284433</td>
<td>3.910049</td>
<td>Tired</td>
</tr>
<tr>
<th>4</th>
<td>-0.000834</td>
<td>0.002970</td>
<td>46.395794</td>
<td>4.436914</td>
<td>Pleased</td>
</tr>
<tr>
<th>5</th>
<td>-0.001896</td>
<td>-0.001654</td>
<td>48.362561</td>
<td>4.013522</td>
<td>Sad</td>
</tr>
<tr>
<th>6</th>
<td>-0.002551</td>
<td>0.000869</td>
<td>59.083402</td>
<td>3.036652</td>
<td>Relaxed</td>
</tr>
<tr>
<th>7</th>
<td>-0.002301</td>
<td>-0.002254</td>
<td>48.161705</td>
<td>5.110528</td>
<td>Pleased</td>
</tr>
<tr>
<th>8</th>
<td>-0.002890</td>
<td>-0.000064</td>
<td>52.981581</td>
<td>4.607283</td>
<td>Afraid</td>
</tr>
<tr>
<th>9</th>
<td>0.000044</td>
<td>0.002082</td>
<td>48.025167</td>
<td>3.730987</td>
<td>Mix</td>
</tr>
<tr>
<th>10</th>
<td>-0.000073</td>
<td>-0.000042</td>
<td>55.873222</td>
<td>4.402845</td>
<td>Afraid</td>
</tr>
<tr>
<th>11</th>
<td>-0.000254</td>
<td>-0.001653</td>
<td>62.410698</td>
<td>6.520325</td>
<td>Sad</td>
</tr>
<tr>
<th>12</th>
<td>-0.001560</td>
<td>0.000646</td>
<td>41.603721</td>
<td>4.267015</td>
<td>Angry</td>
</tr>
<tr>
<th>13</th>
<td>-0.001363</td>
<td>-0.000718</td>
<td>32.500379</td>
<td>3.303371</td>
<td>Angry</td>
</tr>
<tr>
<th>14</th>
<td>-0.002550</td>
<td>-0.001232</td>
<td>53.745451</td>
<td>4.533554</td>
<td>Satisfied</td>
</tr>
<tr>
<th>15</th>
<td>-0.001855</td>
<td>0.001056</td>
<td>53.571594</td>
<td>4.125465</td>
<td>Tired</td>
</tr>
<tr>
<th>16</th>
<td>-0.002170</td>
<td>-0.001059</td>
<td>56.175345</td>
<td>3.739604</td>
<td>Annoyed</td>
</tr>
<tr>
<th>17</th>
<td>-0.000951</td>
<td>0.001410</td>
<td>43.203369</td>
<td>4.116629</td>
<td>Bored</td>
</tr>
<tr>
<th>18</th>
<td>0.000185</td>
<td>0.000682</td>
<td>53.907577</td>
<td>4.237050</td>
<td>Pleased</td>
</tr>
<tr>
<th>19</th>
<td>-0.000184</td>
<td>-0.000246</td>
<td>52.905508</td>
<td>4.148395</td>
<td>Excited</td>
</tr>
<tr>
<th>20</th>
<td>-0.001560</td>
<td>-0.001905</td>
<td>55.523178</td>
<td>4.340211</td>
<td>Happy</td>
</tr>
<tr>
<th>21</th>
<td>-0.001759</td>
<td>0.000900</td>
<td>45.436848</td>
<td>4.257791</td>
<td>Angry</td>
</tr>
<tr>
<th>22</th>
<td>-0.000372</td>
<td>0.002558</td>
<td>57.722183</td>
<td>4.424116</td>
<td>Miserable</td>
</tr>
<tr>
<th>23</th>
<td>0.000884</td>
<td>0.004534</td>
<td>31.542905</td>
<td>3.119212</td>
<td>Miserable</td>
</tr>
<tr>
<th>24</th>
<td>-0.002209</td>
<td>-0.000254</td>
<td>62.365436</td>
<td>6.278034</td>
<td>Relaxed</td>
</tr>
<tr>
<th>25</th>
<td>-0.003495</td>
<td>0.002474</td>
<td>62.691057</td>
<td>6.775984</td>
<td>Annoyed</td>
</tr>
<tr>
<th>26</th>
<td>-0.000142</td>
<td>-0.009252</td>
<td>52.386723</td>
<td>6.254499</td>
<td>Afraid</td>
</tr>
<tr>
<th>27</th>
<td>-0.000601</td>
<td>-0.002673</td>
<td>45.750873</td>
<td>5.537992</td>
<td>Excited</td>
</tr>
<tr>
<th>28</th>
<td>-0.002934</td>
<td>0.005929</td>
<td>35.486262</td>
<td>4.347244</td>
<td>Excited</td>
</tr>
<tr>
<th>29</th>
<td>-0.002131</td>
<td>0.002095</td>
<td>49.055195</td>
<td>5.256263</td>
<td>Happy</td>
</tr>
<tr>
<th>30</th>
<td>0.004173</td>
<td>-0.001804</td>
<td>51.143077</td>
<td>5.439556</td>
<td>Bored</td>
</tr>
<tr>
<th>31</th>
<td>-0.000224</td>
<td>-0.006051</td>
<td>40.074855</td>
<td>3.727305</td>
<td>Happy</td>
</tr>
<tr>
<th>32</th>
<td>-0.002232</td>
<td>0.004002</td>
<td>47.220204</td>
<td>5.129865</td>
<td>Afraid</td>
</tr>
<tr>
<th>33</th>
<td>-0.003202</td>
<td>0.001654</td>
<td>27.594398</td>
<td>3.238834</td>
<td>Annoyed</td>
</tr>
<tr>
<th>34</th>
<td>-0.002317</td>
<td>0.000272</td>
<td>63.977990</td>
<td>4.435240</td>
<td>Bored</td>
</tr>
<tr>
<th>35</th>
<td>-0.002719</td>
<td>0.004786</td>
<td>43.860434</td>
<td>4.161989</td>
<td>Annoyed</td>
</tr>
<tr>
<th>36</th>
<td>-0.000957</td>
<td>0.000309</td>
<td>41.176874</td>
<td>2.883719</td>
<td>Sad</td>
</tr>
<tr>
<th>37</th>
<td>-0.001290</td>
<td>-0.000089</td>
<td>55.583615</td>
<td>5.272462</td>
<td>Tired</td>
</tr>
<tr>
<th>38</th>
<td>-0.000217</td>
<td>-0.004358</td>
<td>49.607502</td>
<td>6.279034</td>
<td>Relaxed</td>
</tr>
<tr>
<th>39</th>
<td>-0.000071</td>
<td>-0.002206</td>
<td>38.600903</td>
<td>5.021533</td>
<td>Satisfied</td>
</tr>
<tr>
<th>40</th>
<td>-0.001090</td>
<td>-0.001596</td>
<td>68.660583</td>
<td>4.984018</td>
<td>Satisfied</td>
</tr>
<tr>
<th>41</th>
<td>-0.000999</td>
<td>0.000668</td>
<td>77.463016</td>
<td>5.703841</td>
<td>Mix</td>
</tr>
<tr>
<th>42</th>
<td>-0.001357</td>
<td>0.000859</td>
<td>54.578165</td>
<td>4.464673</td>
<td>Happy</td>
</tr>
<tr>
<th>43</th>
<td>0.003839</td>
<td>0.004214</td>
<td>42.680804</td>
<td>4.096789</td>
<td>Excited</td>
</tr>
<tr>
<th>44</th>
<td>-0.002007</td>
<td>-0.000875</td>
<td>55.284132</td>
<td>4.743275</td>
<td>Sad</td>
</tr>
<tr>
<th>45</th>
<td>0.004543</td>
<td>0.002699</td>
<td>44.558832</td>
<td>4.904963</td>
<td>Bored</td>
</tr>
<tr>
<th>46</th>
<td>0.000246</td>
<td>0.000620</td>
<td>34.547461</td>
<td>3.294687</td>
<td>Relaxed</td>
</tr>
<tr>
<th>47</th>
<td>-0.000669</td>
<td>0.007457</td>
<td>47.166044</td>
<td>5.101586</td>
<td>Pleased</td>
</tr>
<tr>
<th>48</th>
<td>-0.000959</td>
<td>-0.000093</td>
<td>48.413527</td>
<td>4.118721</td>
<td>Mix</td>
</tr>
</tbody>
</table>
</div>
python
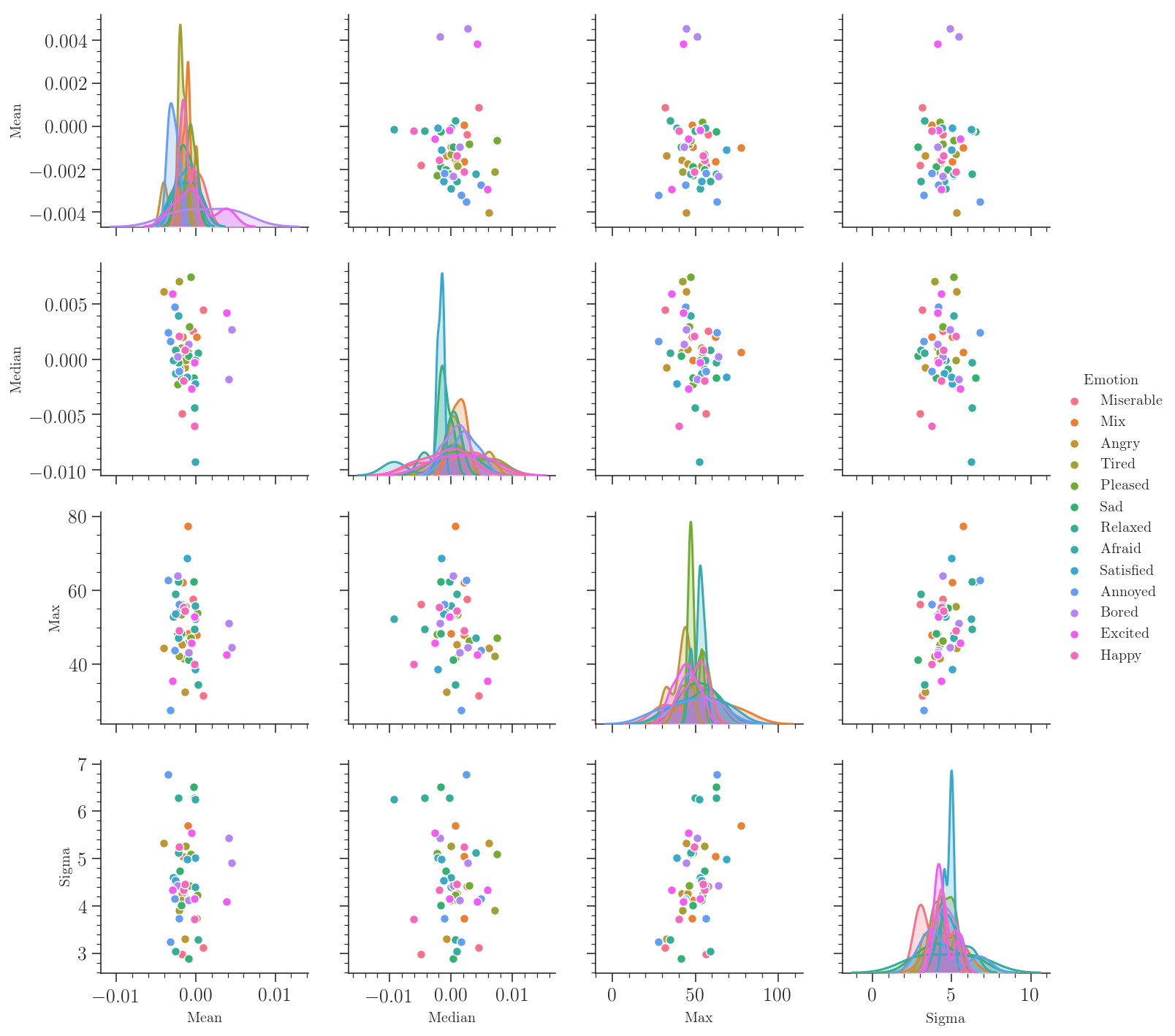
with sns.axes_style("ticks"):
sns.pairplot(df, hue='Emotion')
plt.savefig('Figures/PairPlot.pdf', bbox_inches='tight')
/home/tboudreaux/anaconda3/envs/general/lib/python3.7/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use arr[tuple(seq)] instead of arr[seq]. In the future this will be interpreted as an array index, arr[np.array(seq)], which will result either in an error or a different result.
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
# Periodic Behavior in Velocity
python
FTs_V = np.zeros(shape=(49, 2, 2000))
python
count = 0
for did, dance in tqdm(enumerate(velocities), total=len(velocities)):
if did != 9:
f, pgram = genLSP(dance[0], dance[1], s=2000)
FTs_V[count, 0] = f
FTs_V[count, 1] = pgram
count += 1
python
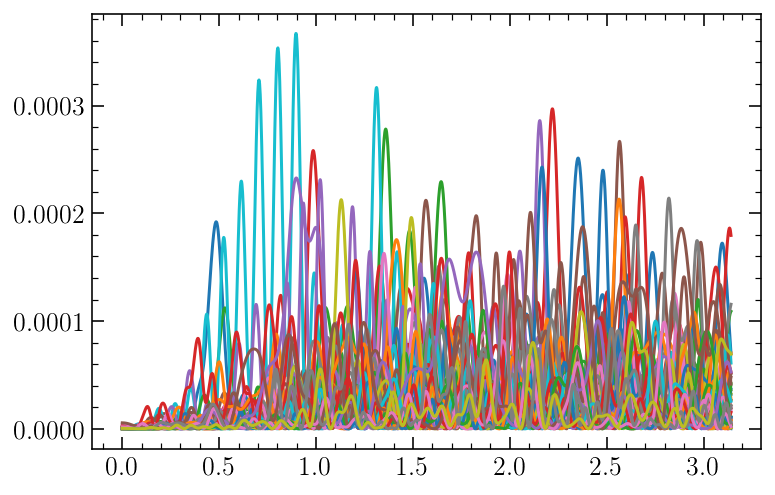
for fid, FT in enumerate(FTs_V):
plt.plot(FT[0], FT[1])
python
stats_V = np.zeros(shape=(49, 3))
count = 0
for fid, FT in enumerate(FTs_V):
stats_V[count] = np.array([FT[0][FT[1].argmax()], FT[1][FT[1].argmax()], np.mean(FT[1])])
count += 1
python
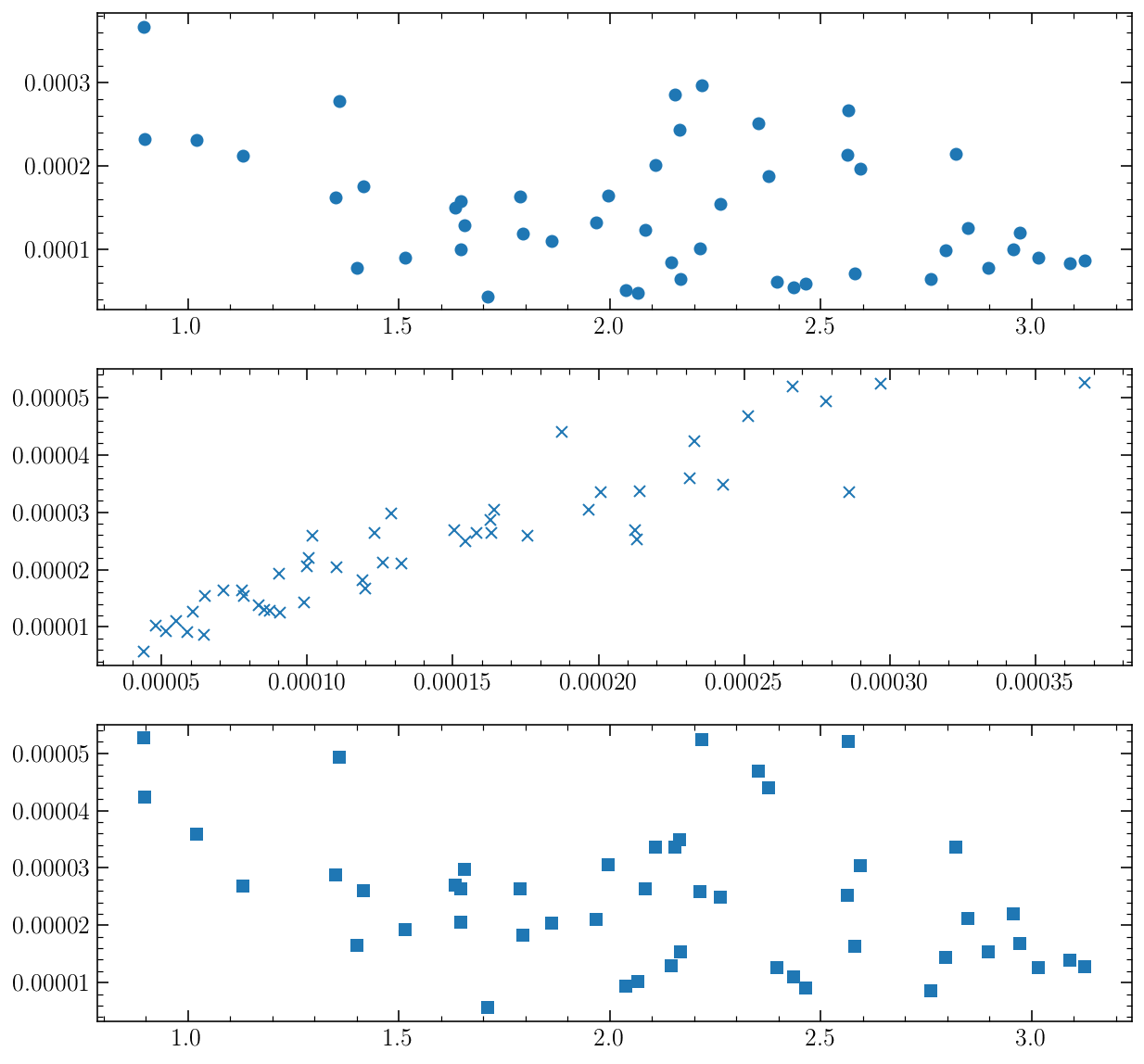
fig, axs = plt.subplots(3, 1, figsize=(10, 10))
axs[0].plot(stats_V[:, 0], stats_V[:, 1], 'o')
axs[1].plot(stats_V[:, 1], stats_V[:, 2], 'x')
axs[2].plot(stats_V[:, 0], stats_V[:, 2], 's')
[<matplotlib.lines.Line2D at 0x7fed82866c88>]
python
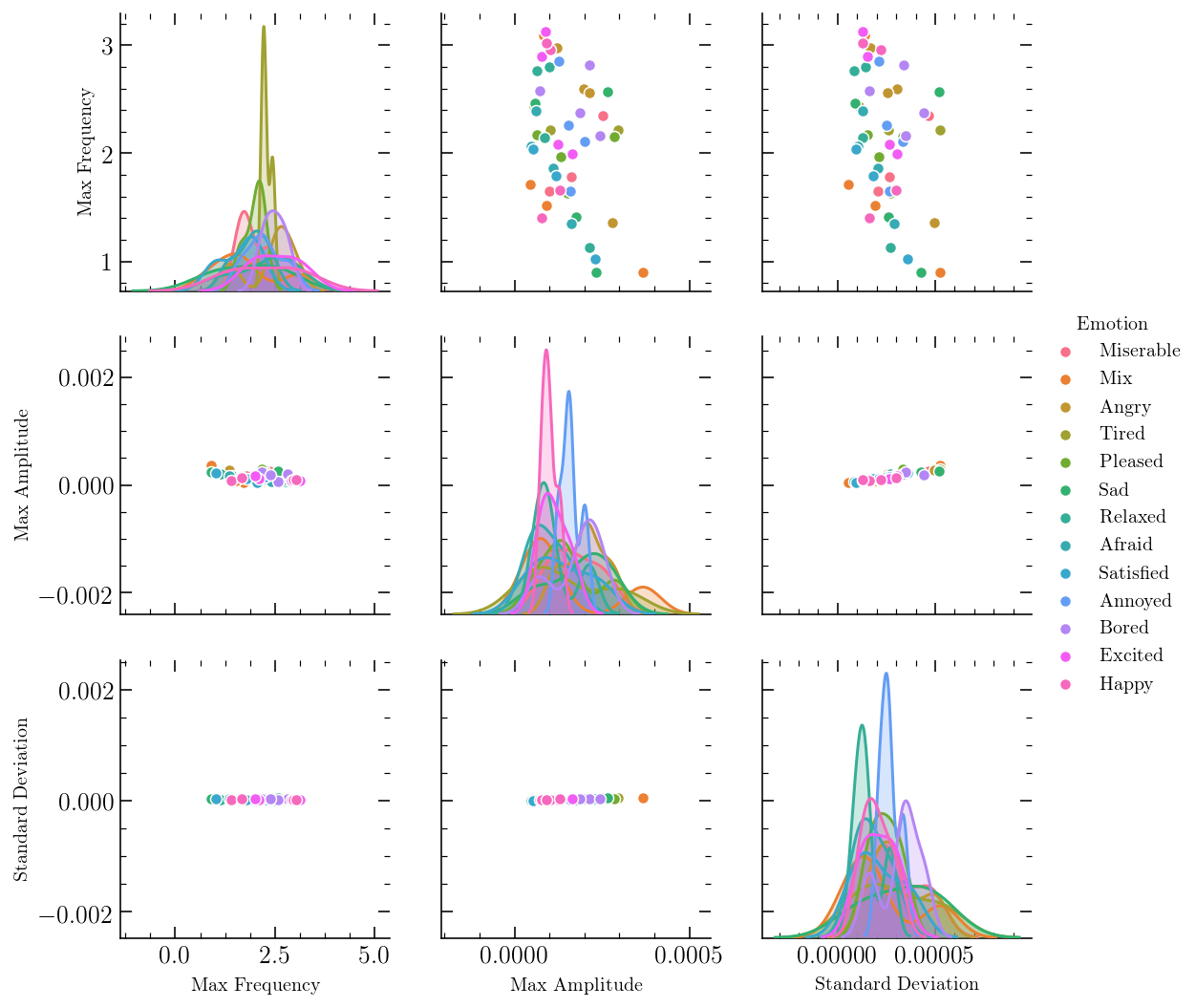
df = pd.DataFrame(data=stats_V, columns=['Max Frequency', 'Max Amplitude', 'Standard Deviation'])
df['Emotion'] = pd.Series(evalEmotions, index=df.index)
python
sns.pairplot(df, hue="Emotion")
/home/tboudreaux/anaconda3/envs/general/lib/python3.7/site-packages/scipy/stats/stats.py:1713: FutureWarning: Using a non-tuple sequence for multidimensional indexing is deprecated; use arr[tuple(seq)] instead of arr[seq]. In the future this will be interpreted as an array index, arr[np.array(seq)], which will result either in an error or a different result.
return np.add.reduce(sorted[indexer] * weights, axis=axis) / sumval
<seaborn.axisgrid.PairGrid at 0x7fed80383ba8>
python